A guy notices a bunch of targets scattered over a barn wall, and in the center of each, in the “bulls-eye,” is a bullet hole. “Wow,” he says to the farmer, “that’s pretty good shooting. How’d you do it?” “Oh,” says the farmer, “it was easy. I painted the targets after I shot the holes.” – An Old Joke
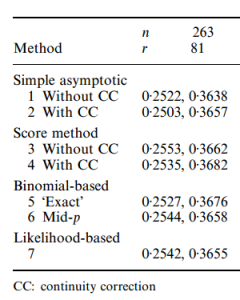
Last year I dumped piece of SAS codes to compute confidence intervals for single proportion using 11 methods including 7 presented by one of Prof. Newcombe‘s most wildly cited papers, Two-sided confidence intervals for the single proportion: comparison of seven methods (r is the number of event in total cases of n):
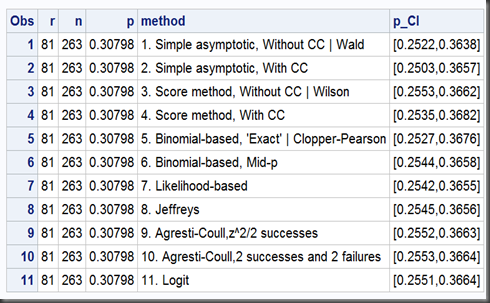
To get such results using my macro, just submit the following SAS codes:
filename CI url ‘https://raw.github.com/Jiangtang/Programming-SAS/master/CI_Single_Proportion.sas’;
%include CI;
%CI_Single_Proportion(r=81,n=263);
And the outputs(plus 4 additional methods):
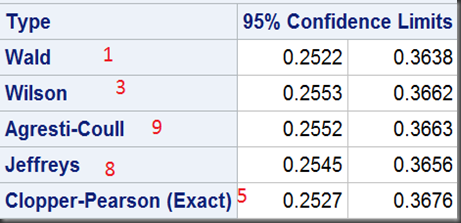
In SAS 9.2 and 9.3, 6 of the 11 intervals can be calculated by PROC FREQ. First, method 1, 3, 9 ,8, 5 via a binomial option:
data test;
input grp outcome $ count;
datalines;
1 f 81
1 u 182
;ods select BinomialCLs;
proc freq data=test;
tables outcome / binomial(all);
weight Count;
run;
The outputs:
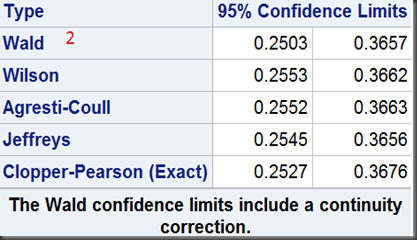
And you can get another Wald interval with a continuity correction (method 2) via binomialC option:
ods select BinomialCLs;
proc freq data=test;
tables outcome / binomialc(all);
weight Count;
run;
get:
R Notes
These two R packages contain a bunch of CI calculations:
For SAS macro %CI_Single_Proportion, I borrowed a lot from this R implementation:
http://www2.jura.uni-hamburg.de/instkrim/kriminologie/Mitarbeiter/Enzmann/Software/prop.CI.r
Additional Notes
If interested, a nice paper on binomial intervals with ties, the paper Confidence intervals for a binomial proportionin the presence of ties, and the program.