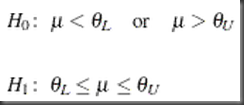_Programmers Need to Learn Statistics Or I will Kill Them All –Zed A. Shaw_
In an equivalence testing example against lognormal data, a TOST (Two One-Sided Test) option used in SAS TTEST procedure:
proc ttest data=auc dist=lognormal tost(0.8, 1.25);
paired TestAUC*RefAUC;
run;
And the output:
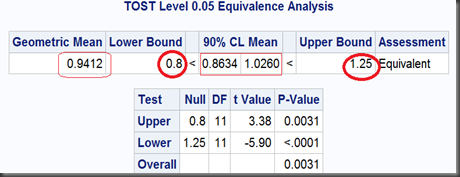
Since the 90% (who not 95%? see below) limit of the geometric mean ratio (0.9412) , [0.8634,1.0260], lies in the FDA endorsed equivalence bounds [0.8,1.25], then we can make a conclusion of “Equivalent” among these Test and Reference drugs. Following are the notes on how this so called TOST (Two One-Sided Test) works.
In its original form, the hypothesis of equivalence testing is written as difference on means (equivalence by definition: not above the upper limit, and not below the lower limit):
Since our AUC example with lognormal data, the difference on means is transformed into a ratio, geometric mean ratio: if no difference in means, then the ratio simply equals 1. The two one-sided tests are (with form of ratio, not difference anymore):
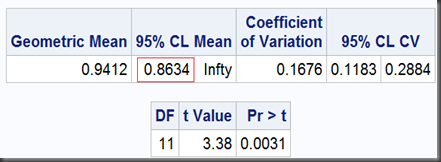
I) upper one-sided T-test with a null ratio as the left bound of predefined limits, here is 0.8
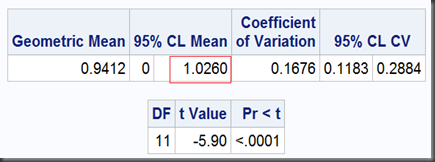
II) lower one-sided T-test with a null ratio as the right bound of predefined limits, here is 1.25.
T-test I can be done as (with option sides=U, where U means upper one-sided test. This option also only goes with SAS 9.2 and later)
proc ttest data=auc dist=lognormal h0=0.8 sides=U;
paired TestAUC*RefAUC;
run;
And the output:
T-test II, lower one-sided (with option sides=L, where L means lower one-sided test):
proc ttest data=auc dist=lognormal h0=1.25 sides=L;
paired TestAUC*RefAUC;
run;
And the output:
So, the two one-sided tests together get a limit of [0.8634,1.0260], which is exactly as same as we got before using TOST option, except the former noted as “95%” and the later, “90%”. That’s because, the 0.1 (1-90%) should be dividend by 2 for the two one-sided tests to ensure they can both get their 0.05 significance respectively. Namely, at significant level α=5%, the equivalence test gets a 100(1-2α)% = 90% interval.
At last, the overall P-value, will take the maximum one in these two one-sided tests (here we get max{0.0031,<0.0001} = 0.0031).
SAS Notes
Just did a quick search, PROC MIXED seemed more popular for statisticians to perform equivalence test years before:
Cookbook SAS Codes for Bioequivalence Test in 2x2x2 Crossover Design, by Chunqin Deng (2012)
_The Paired T-Test: Does PROC MIXED Produce the Same Results as PROC TTEST?_ by Jack Nyberg (2004)
Section 8.2 Bioequivalence Testing, in __Pharmaceutical Statistics Using SAS: A Practical Guide, by Alex Dmitrienko, Christy Chuang-Stein, and Ralph D’Agostino (2007)